1.物理意义:
平均速度:描述物体在一段时间(或一段位移)内位置改变的平均快慢及方向,过程量;
平均速率:描述物体沿轨迹运动的平均快慢,过程量;
瞬时速度:描述物体在某一时刻(或者某一位置)的运动快慢及方向,状态量;
瞬时速率:瞬时速度大小,状态量。
☞对应一段时间或一段位移的物理量就是过程量,如冲量、功、位移等;对应一个时刻或一个位置的物理量就是状态量,如动量、能量、温度等。
2.标矢性:
平均速度:矢量,方向与位移方向相同;
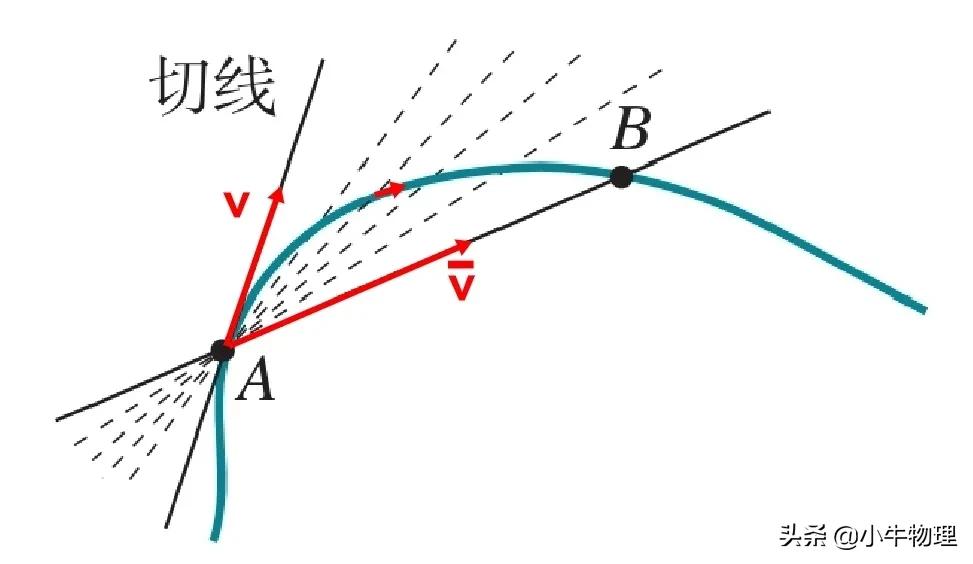
瞬时速度:矢量,方向沿轨迹切线方向;
平均速率:标量,无方向;
瞬时速率:标量,无方向。
3.大小:
平均速度:平均速度=位移/时间,定义式v=△x/△t(△t为一段时间);
瞬时速度:△t→0的平均速度,定义式v=△x/△t(△t→0的极限);
平均速率:平均速率=路程/时间,单向直线运动平均速率等于平均速度大小;
瞬时速率:瞬时速度的大小。
4.平均速度和瞬时速度的联系
(1)瞬时速度等于运动时间△t→0时的平均速度;
(2)对于匀速直线运动,瞬时速度与平均速度相等
5.注意
①平均速度不是速度平均值;
②平均速度有公式△x/△t,瞬时速度理论上求极限,测量时只能用极短时间内平均速度粗略代替瞬时速度,时间越短越接近真实的瞬时速度,用到了数学的极限思想,如果做匀变速直线运动,就可以求真实值,通常用在打点计时器的纸带问题、光电门求速度;
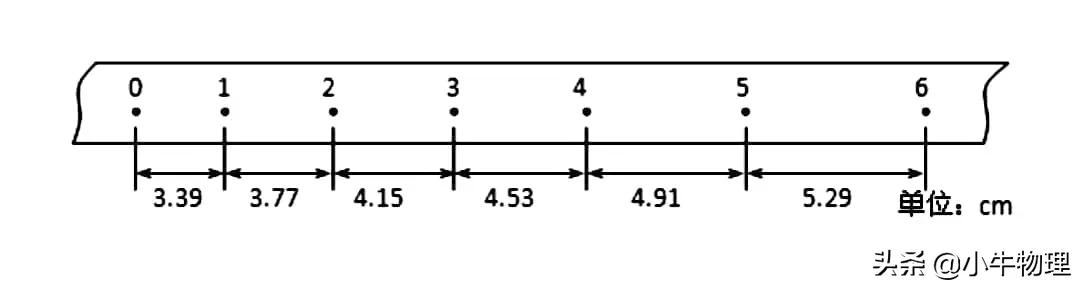
求点4的速度用3-5点平均速度代替,用2-6点平均速度精确度更差,因为时间更长了,如果纸带做匀变速直线运动,那瞬时值就是准确的。
③瞬时速度一直保持不变的运动就是匀速直线运动;
④瞬时速度大,平均速度不一定大;
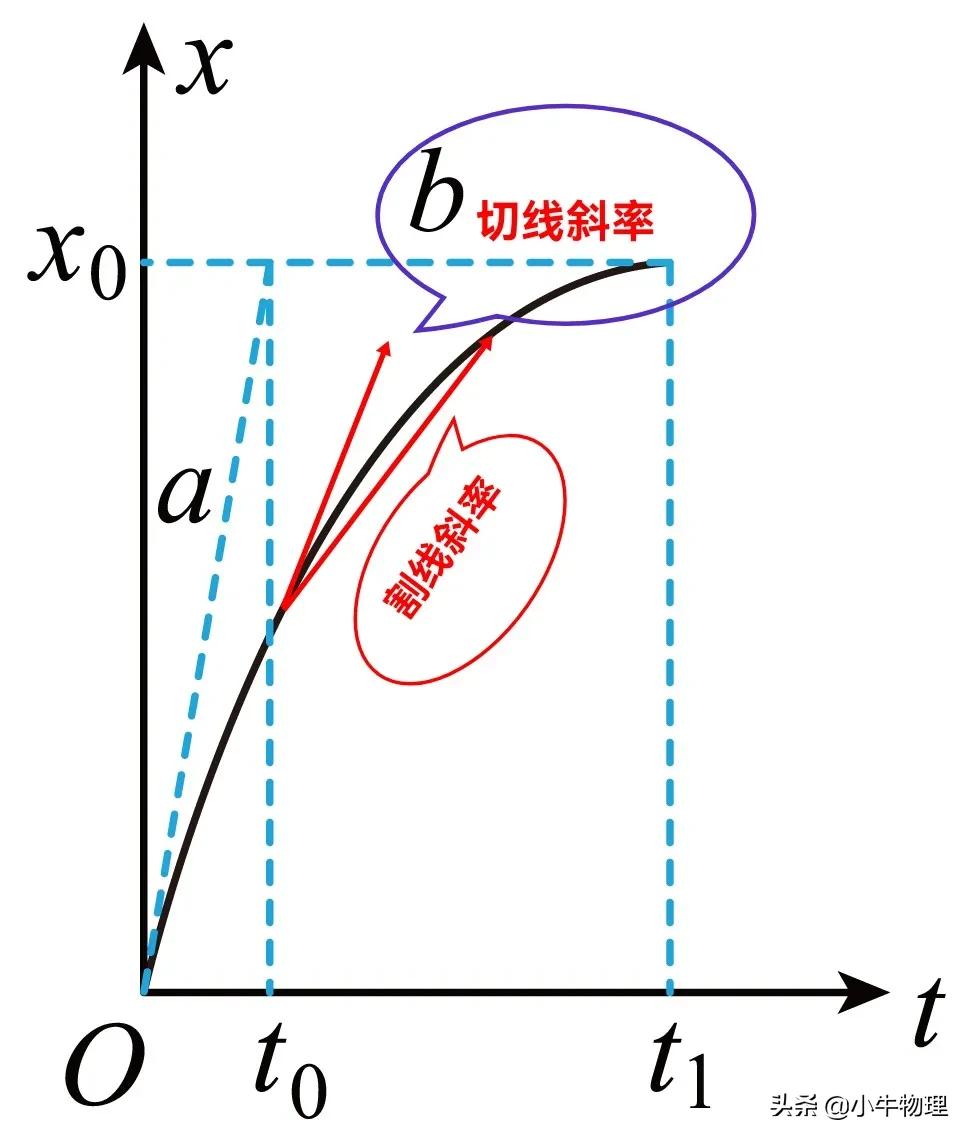
⑤x-t图中,切线斜率表示瞬时速度,割线斜率表示平均速度;
⑥理论上求瞬时速度
a.匀变速直线运动,用运动学关系式;
b.有速度表达式的,代入时间直接求;
c.有位移表达式的,求极限或对时间求导;
d.有x-t图的,求斜率;
e.有v-t图的,直接看。
例1:关于平均速度和瞬时速度,以下说法正确的是( CDE)
A.平均速度就是速度的平均值
B.平均速率就是平均速度的大小
C.瞬时速率就是瞬时速度的大小
D.瞬时速度一直保持不变的运动就是匀速直线运动
E.匀速直线运动任一过程的平均速度都等于其瞬时速度
☞绕操场一圈,平均速度为0。
例2:(1)一物体做同向直线运动,前一半时间以9m/s的速度做匀速运动,后一半时间以6m/s的速度做匀速运动,则全程物体的平均速度是多大?
(2)另一物体也做同向直线运动,前一半路程以3m/s的速度做匀速运动,后一半路程以7m/s的速度做匀速运动,则全程物体的平均速度是多大?
☞平均速度不是速度平均值。
例3:质点沿直线Ox方向做变速运动,它离开O点的距离x随时间t变化的关系为x=(5十2t³)m,该质点在t=2s到t=3s间的平均速度的大小及t=2s时的瞬时速度大小分别为___。
☞用求导方法求瞬时速度。
例4:气垫导轨上滑块经过光电门时,其上的遮光条将光遮住,电子计时器可自动记录遮光时间△t。测得遮光条的宽度为△x,用△x/△t近似代表滑块通过光电门时的瞬时速度。为△x/△t使更接近瞬时速度,正确的措施是(A)
A.换用宽度更窄的遮光条
B.提高测量遮光条宽度的精确度
C.使滑块的释放点更靠近光电门
D.增大气垫导轨与水平面的夹角
☞用平均速度(宽度除以时间)代替瞬时速度,理论上宽度越窄,时间越短,瞬时速度越接近真实值,但是宽度越窄,宽度测量误差更大,瞬时速度反而离真实值更远。
例5:一身高为H的田径运动员正在参加百米国际比赛,在终点处,有一位站在跑道终点旁的摄影记者用照相机给他拍摄冲线过程,摄影记者使用的照相机的光圈(控制进光量的多少)是16,快门(曝光时间)是1s/60,得到照片后测得照片中运动员的高度为h,胸前号码布上模糊部分宽度是△L.由以上数据可以知道运动员的(BD)
A.百米成绩
B.冲线速度
C.百米内的平均速度
D.冲线时1s/60内的位移
☞如同地图,要按比例。
例6:用如图所示的计时装置可以近似测出气垫导轨上滑块的瞬时速度.已知固定在滑块上遮光条的宽度为4.0mm,遮光条经过光电门的遮光时间为0.040s,则滑块经过光电门位置时的速度大小为(A)
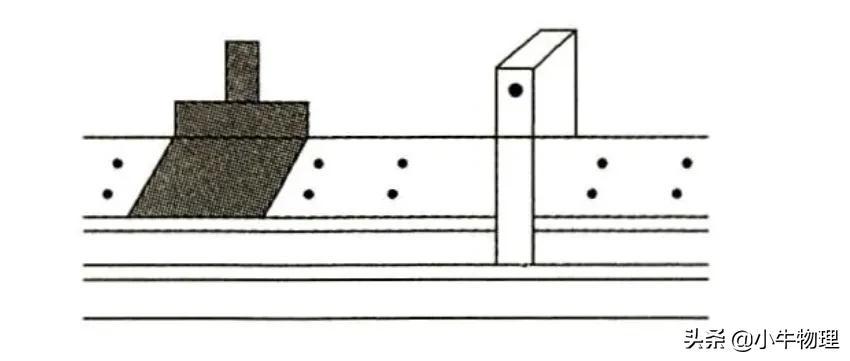
A.0.10m/s
B.100m/s
C.4.0m/s
D.0.40m/s
☞光电门上或纸带上的应用。